f /(1-f) = n0t burn <s DT v>/2 (4)
Why Magnetized Target Fusion Offers
A Low-Cost Development Path
for Fusion Energy
Richard E. Siemon
Irvin R. Lindemuth
Kurt F. Schoenberg
Los Alamos National Laboratory
Los Alamos, New Mexico
Submitted to Comments on Plasma Physics and Controlled Fusion, November 12, 1997
I. Introduction
Reasonably priced energy supplies have become an expectation of the developed world and a necessary ingredient for development of Third World countries. The problem of providing large supplies of low-cost energy is a long-term, complex one that requires sustained R&D efforts, in spite of the shadow cast on long-term R&D by the federal deficit problem. The role of fusion energy as a power source was thoroughly reviewed and strongly endorsed in 1995 by the President’s Committee of Advisors on Science and Technology Fusion Review Panel chaired by John Holdren. He argued [Holdren 95]:
The options available for meeting the world’s demand for energy in 2050 and beyond are those already in use – fossil fuels, biomass energy, nuclear fission, hydropower, geothermal energy, wind energy, and solar energy – plus, potentially, nuclear fusion.
In these circumstances, it should be obvious that there is great merit in the pursuit of diversity in energy options for the next century. There are not so many possibilities altogether. The greater the number of these that can be brought to the point of commercialization, the greater will be the chance that overall energy needs can be met without encountering excessive costs from or unmanageable burdens upon any one source.
In the past decade the critical issue for fusion has shifted from one of scientific feasibility to one of commercial viability. The specific problem is that all fusion technologies currently being pursued involve extremely costly facilities for the required steps of further development. In the present international fiscal environment, it is imperative to find a more cost effective development path for fusion energy.
The conventional regime of Magnetic Fusion Energy (MFE), with plasma density n ~ 1014 cm-3 and magnetic field provided by superconducting magnets, has been relatively well explored [Sheffield 96]. Tokamaks are the major devices studied in MFE, and tokamak research has tremendously advanced our understanding of plasma physics. The International Tokamak Experimental Reactor (ITER) design illustrates the technology and cost for an ignited plasma demonstration in the MFE regime. The estimated $10-billion price for ITER calls into question whether fusion can ever be developed based on tokamak-like technology. Factors of a few, or maybe ten at most, in any parameter such as size, neutron wall loading, and so forth are about all that one can credibly seek in optimizing a tokamak system. Certainly research seeking to reduce the ITER-like system size by factors of a few is extremely important and needs to be pursued. But we strongly suspect that the necessary breakthrough, which would allow fusion to be developed in a more timely and affordable manner, will involve a qualitatively different and significant departure from the MFE tokamak regime and technology.
Another approach to fusion, Inertial Confinement Fusion (ICF), represents a good alternative to MFE in that the regime of density and pressure is completely different, the physics issues are quite distinct, and the technology required has fairly little in common with a tokamak-like system [Lindl 95]. Thus, the issues that are likely to emerge as limitations for one approach are unlikely to apply to the other. Unfortunately, the cost of developing ICF is also high. The price of the National Ignition Facility (NIF), which will demonstrate ICF ignition, is over $1 billion. The anticipated cost of developing efficient inertial fusion drivers such as heavy ion beams is also high [Bangerter 97]. For the development of fusion energy, something less expensive would obviously be desirable.
A Lower Cost Alternative—Magnetized Target Fusion
To find a lower cost approach, we start by noting that the cost of development is directly linked to the system size, which in the case of MFE is mostly dictated by the maximum magnetic field strength obtainable with superconducting magnets. The critical constraint with ICF is the costly high-power drivers needed to achieve the extreme conditions of density and pressure.
We also note that countless examples can be found in the magnetic fusion literature showing that fusion reactions can be created in smaller-sized systems if one admits larger magnetic field, higher plasma density, and pulsed operation as with imploding liners [Sherwood 81, Lindemuth 83, Robson 76, Vekshtein 90, Ryutov 96, Gross 76]. In this paper we will review the basic reason for that tendency, and examine some of the consequences. We will conclude that the most interesting regime of density is n ~1020 cm-3, which is high compared with MFE, but low compared with ICF. This density regime at 10 keV temperature corresponds to megabars of pressure (millions of atmospheres), which is intrinsically pulsed in nature.
We define the intermediate density regime to be Magnetized Target Fusion (MTF). The name is chosen based on two general characteristics that we assume for MTF: 1) as with ICF, PdV work heats the fuel by compressing it inside an imploding wall, or "pusher" in the parlance of ICF, and 2) magnetic field is embedded in the fuel to insulate it from the pusher.
Although numerous variations in approach can be envisioned, we have in mind the magnetically-driven imploding liner method for MTF. In the liner approach:
The liner velocity required is termed hypervelocity because the kinetic energy density exceeds the heat of vaporization for liner materials. The technology for precision implosions creating millions of atmospheres of pressure is a challenge in its own right. In the 1970s when a number of MTF-related efforts were underway, most of the effort was directed towards developing this demanding technology, and very few integrated tests with a preheated plasma were ever done. In what must be viewed as a serendipitous coincidence, the Department of Energy's Office of Defense Programs (DP) in the last decade has significantly advanced the technology of imploding liners with the same parameters of implosion velocity and kinetic energy as those needed for investigating fusion reactions in the MTF regime. The purpose of the Defense Program work is to study and understand hydrodynamics in the megabar pressure regime and has no connection with nuclear fusion. However, the existence of DP expertise and facilities offers an important near term advantage for resuming MTF research.
The magnetic field to insulate fuel from its surroundings is the essential ingredient of MTF. In fact, the benefit of a magnetic field in a fusion target was recognized in the 40’s by Fermi at Los Alamos and at approximately the same time by Sakharov in the former Soviet Union. We will derive below the advantages in terms of reduced energy and power that must be delivered to the fusion fuel. The advantages of MTF can also be expressed in terms of requirements on driver technology. By preheating MTF fuel to between 100 and 500 eV, the volume compression needed to reach 10 keV temperature is 100-1000. The volume compression ratios for ICF are typically 30,000 to 60,000, which requires a much more precise implosion system. The characteristic implosion velocity for MTF is 0.3-3.0 cm per microsecond, which is 10 to 100 times smaller than for ICF. The peak pressure for MTF is 1-10 megabars, and for ICF, 100s of gigabars. These impressive differences justify careful examination of ways to introduce a magnetic field.
II. The Technical Case for Magnetized Target Fusion
A. Lawson Condition for Pulse Duration and Energy Confinement Time
In a pulsed system, as opposed to steady-state, the pulse duration, t burn, is an important new variable. The pulse duration determines the amount of fuel that reacts or "burns," given the reaction cross section, leading to an nt burn requirement in a similar way that nt E is determined from power balance in a steady-state system. For deuterium (DT) fuel the thermonuclear reaction rate per unit volume is
R = nDnT <s DT v> = 1/4 n2 <s DT v> (1)
where nD=nT is the deuterium and tritium density, n =nD+nT is the total ion or electron density, and <s DT v> is the averaged product of cross section and relative velocity for a Maxwellian velocity distribution. At 10 keV, <s DT v> @ 10-16 cm3/sec. The total density decreases at the rate 2R as the fuel is consumed, and the frequency of fusion reactions per ion for either deuterium or tritium ions is given by 2R/n:
(dnD/dt)/nD = (dn/dt)/n = ½ n <s DT v> (2)
Assuming for simplicity that DT fuel is held at constant temperature so that <s DT v> is constant in time while it burns, Eqn. 2 can be integrated to give
n/n0 = 1/(1+ n0t burn <s DT v>/2) (3)
where t burn is the burn time. Equation 3 can be recast in terms of f, the fractional burnup of fuel, as:
f /(1-f) = n0t burn <s DT v>/2 (4)

where f º 1-n/n0. For complete burnup, the gain would be Gmax= 300 at 10 keV. This is simply the ratio of energy for a 14.1 MeV neutron and 3.5 MeV alpha divided by the
60 keV of thermal energy for a DT ion pair with electrons.
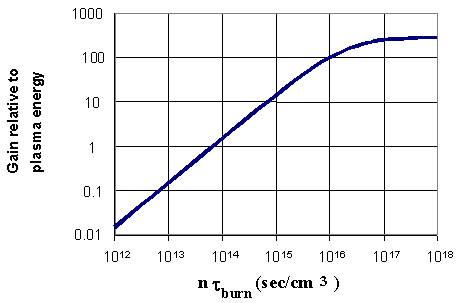
Figure 1. Fusion energy output relative to plasma energy vs. the product of density and burn time.
As a function of burn time, the gain plotted in Fig. 1 is Gmax times the fractional burnup. We can define a Lawson condition using Fig. 1. With nt burn ~ 3x1014 cm-3 sec the gain relative to thermal energy is around five, enough to allow for net gain with realistic efficiencies. The net gain relative to initially stored electrical energy is the gain of Fig. 1 times the efficiency of heating fuel to 10 keV temperature. For example, if 50% of the stored electrical energy is converted to liner kinetic energy [Gerwin 78], and 50% of the liner kinetic energy is converted to thermal plasma energy at peak compression, then the net gain would be 1/4 of the gain plotted in Fig. 1.
A plasma heated to 10 keV will cool by numerous mechanisms. The total power losses per unit volume are conventionally written as 3nT/t E, where t E is the global energy confinement time. In deriving Fig. 1 we ignored losses, which is equivalent to assuming
t E>>t burn. To obtain the minimum possible system size for the purpose of low–cost development, we would require t E ~ t burn . That is, if t E were much less than t burn the fuel would cool before it burned. On the other hand if t E were much larger than t burn , the plasma should be made smaller to equalize the two, which requires less energy, assuming the energy confinement time increases with system size. For approximate estimates, the relevant energy confinement time and the burn time should both satisfy a Lawson-like nt , which we will take for the purposes of demonstrating feasibility to be the same as ITER, and approximately an energy breakeven condition according to Figure 1:
Lawson requirement: nt ~ nt E ~ nt burn ~ 3x1014 cm-3 sec
This nt E corresponds to 1.5% burnup fraction in a pulsed system.
B. Pressure of High-Density Fuel Dictates Pulsed Technology
The first requirement for containing fuel is equilibrium or pressure balance to prevent the fuel from expanding during the required burn time. There are a continuum of possibilities ranging from ICF with zero magnetic field where pressure is supported by the inertia of surrounding low-temperature fuel, to full magnetic confinement where plasma pressure is less than or equal to the confining magnetic pressure. In the MTF regime we consider the possibility where plasma pressure is larger than or equal to the magnetic field pressure, because the main role of magnetic field is insulation and not confinement.
Broadly speaking, the relevant technology changes as the density increases. We assume Ti ~ Te ~ 10 keV. At densities from 1014 cm-3 up to about 1016 cm-3 plasma pressure can be contained by superconducting magnets, where the higher density corresponds to magnetic confinement with b = 1. Plasma b º 2nkT/(B2/8p ), where B is the magnetic field. At pressure or density too high for superconductors, pulsed magnets can be used up to pressures that fracture known materials. Strength limitations set an upper limit on the density at about 1018 cm-3. This density corresponds to magnetic field of about 1 MG if magnetic pressure confines the plasma. To date, the largest magnetic fields reported are pulsed fields of about 20 MG, which can be obtained by imploding liners [Pavlovskii 96]. If 20 MG were used for plasma confinement, the corresponding maximum density is around 1021 cm-3. Above that density, plasma pressure must be held by the inertia of material walls, although magnetic field can be utilized for its insulating properties. For ICF the density of the ignited hot spot is expected to be about 1025 cm-3, which corresponds to a pressure of 200 Gbar. We see that the technology for fusion changes radically as one moves from MFE density to ICF density.
C. Fusion Fuel Diffuses Before Burning
Another basic point useful to recall for the following discussion is that s DT, the cross section for fusion, is much smaller than s C, the cross section for Coulomb scattering, almost independent of density. By definition the frequency of collisions is given by the product of cross section and flux. The rate of fusion reactions is given by the right–hand side of Eqn. 3:
Frequency of fusion reactions = ½ n <s DT v> (5)
The effective fusion cross section can be taken as <s DT v>/vi, ~ 1 barn (10-24 cm2) at
10 keV where vi is the ion thermal speed. Similarly the Coulomb collision frequency can be written as a product of the Coulomb cross section and particle flux, n multiplied by vi:
Ion-ion Coulomb collision frequency = n ii = 1/ t ii = n vis C (6)
Thus at 10 keV and 1014 cm-3 s C ~ 7000 barns. This Coulomb collision frequency, or reciprocal of the ion-ion collision time, is extensively discussed in the standard textbooks. Because of the accumulated effects of small-angle scattering, the frequency of Coulomb collisions is proportional to lnL , a factor that depends weakly upon temperature and density. The Coulomb logarithm is often taken as a constant about equal to 20, but even for rough estimates we will calculate lnL when it arises, because the range of density we will consider (1014–1026 cm-3) corresponds to lnL changing by more than a factor of 3.
At a temperature of 10 keV, the cross section or frequency for Coulomb scattering is larger than the cross section or frequency of fusion reactions by a factor of 2000-6000 for density between 1026 cm-3 and 1014 cm-3 respectively. Therefore, the number of collisions (N) that occur during a burn time is calculated to be:
N = t burn / t ii = 2 f vis C / <s DT v> (7)
For nt E = 3x1014 cm-3 sec, the burn time is between 60 and 180 ion-ion collision times as density varies from 1026 cm-3 to 1014 cm-3.
In summary, we conclude that, independent of the fuel density over a wide range of density, collisional diffusive processes are unavoidable when fusion fuel is assembled for a time long enough to produce energy gain.
D. The Nature of Energy Diffusion
Even if fuel is held in pressure balance for the necessary burn time, it has been historically difficult to achieve the required global energy confinement time. Much of MFE fusion research has been devoted to understanding the many modes of plasma motion that transport energy in addition to classical collisional processes. With ICF, there is less uncertainty about loss processes, because the absence of a magnetic field simplifies the transport physics. In that case electron thermal conduction is the dominant loss process. In the ICF approach parameters are chosen so that even electron thermal conduction is consistent with the Lawson condition. One could say that ICF is the "worst case" for thermal losses when compared with any type of magnetic configuration.
Classical diffusion. We review now the lower bound on energy confinement represented by classical diffusion. In MFE fusion literature, the global energy confinement time is usually expressed in terms of thermal diffusivity:
t
E ~ a2/c , (8)where a is the characteristic dimension across which heat diffuses and c is the thermal diffusivity. The value of c (same as thermal conductivity divided by density) is derived by calculating the energy flux in the presence of a temperature gradient.
Thermal diffusion can also be viewed as a random walk of particles. After each collision, a particle moves one step at random either up or down the temperature gradient. Heat conduction is the diffusion of cold particles up the gradient and hot particles down the gradient with no net flux of particles. The essential feature of the random walk is that after N collisions, there is a binomial distribution for particle location, and it has a width proportional to N1/2. If the step size is l , then the standard deviation of the distribution of particle locations after N collisions is a given by
a = N1/2 l . (9)
If the collision time is t , the number of collisions is N = t / t , so we can also write Eqn. 9 as
t = (a/l )2 t (10)
Eqn. 9 indicates that if N collisions are needed before heat dissipates, then the fuel must have a characteristic size greater than a. Equivalently, Eqn. 10 gives the time to dissipate heat (energy confinement time) in terms of the number of steps across the characteristic size, (a/l ), and the time per step or collision time.
Classical diffusion without a magnetic field. To apply the random-walk argument to electron thermal conduction, we equate the step size to a plasma mean free path l . Electrons have a larger thermal speed and a shorter collision time, such that the mean free path l is the same for either ions or electrons:
l
= 1 / ns C = vi t ii = ve t ee (11)where vi,e is the ion, or electron, thermal speed. Electrons collide more frequently by a factor of (mi/me)1/2 , or about 60 for a DT mixture. Therefore, if we consider high density where ions make about 60 collisions, then electrons make about 3600 collisions during the fusion burn time. The size of a plasma with burn time long enough to allow 3600 electron-electron collisions is
a = (3600)1/2 l . (12)
For ICF, where the ignition hot spot density is about 1025 cm-3, the mean free path is
0.7 microns; this simple estimate of Eqn. 12 for hot spot radius is 42 microns. More detailed calculations [Lindl 95] give about the same value.
Classical diffusion with a magnetic field. To apply the random-walk argument to magnetized plasma is more difficult, because the step size depends upon complicated particle orbits in the magnetic field. However, for poloidal-field dominated configurations like the Reversed Field Pinch, the spheromak, and the Field-Reversed Configuration (FRC), and for tokamaks, detailed studies give the simple prescription that the step size can be taken as the ion gyro radius calculated in the poloidal magnetic field [Boozer 83]. (In a torus the toroidal direction is the long way around the torus, and the poloidal direction is the short way around.) In the direction perpendicular to a magnetic field, the classical ion heat conduction dominates because the ions have a larger gyro radius. Therefore, we can estimate that the minimum required size of a fusion system to diffuse heat slowly enough to meet Lawson, say 180 ion-ion collision times, is
a = (180)1/2 ri, (13)
where ri is the ion gyro radius in the poloidal magnetic field. The tokamak banana-regime formulas for neoclassical transport theory give about 20 ri instead of the approximate estimate of 13 ri given by Eqn. 13. Because of anomalous transport, the design radius of ITER is about 5 times larger than the neoclassical limit (i.e. aiter @ 100 ri).
E. Characteristic Step Sizes Decrease as Density Increases
Comparing Eqns. 8 and 10, we see that c has the form of a step size squared times a collision frequency. For classical transport,
Electron thermal conduction: c e ~ l 2n ee. (14)
Ion cross field transport: c i ~ ri 2n ii. (15)
The mean free path (l ), which depends on temperature and density, is plotted in Fig. 2 for 10 keV temperature. The gyro radius (ri), which depends mainly on density, is also plotted in Fig. 2, assuming constant poloidal beta (b i), where b i is the ratio of ion pressure to poloidal field pressure (b i = 8p nkTi/Bp2). The density dependence can be seen by writing the gyro radius as:
ri = vi/w ci = (c/w pi)b i1/2 (16)
where w ci is the ion cyclotron frequency in the poloidal magnetic field, c is the speed of light, and w pi is the ion plasma frequency,
w pi = (4p ne2/mi)1/2 (cgs units). (17)
Poloidal beta in tokamaks and the above mentioned configurations is observed not to differ much from unity.
In the spirit of a survey of minimum system size for fusion, Fig. 2 gives useful guidance. The dimensions of a system without magnetic insulation become unacceptably large at low density. The classical limit for the size of a magnetized plasma is seen to be quite small as density increases. If the anomaly factor assumed in the ITER design, and observed with tokamaks having density in the vicinity of 1014 cm-3, were to apply at higher density, then Lawson should be possible at 1020 cm-3 in a tokamak with a minor radius of 2.8 mm! This dramatic reduction in size at higher density provides much of the motivation for MTF.
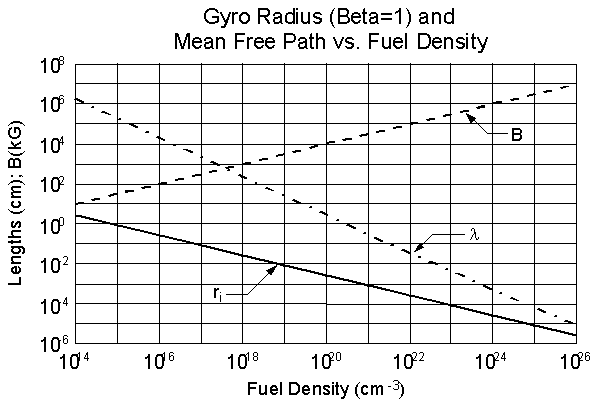
Figure 2. Plots of characteristic step sizes and poloidal magnetic field strength assuming poloidal beta = 1 vs. fuel density for a plasma with 10 keV temperature.
Speculation on anomalous transport. Anomalous transport mechanisms are still a subject of unfinished research. Clearly, all possibilities cannot be anticipated, but the following can be noted. Generally the form of c is a product of characteristic lengths times a frequency. The characteristic lengths in a plasma normally identified are l , l D,
c/w pi, c/w pe, ri, and re. As already noted, c/w pi and ri are only different by a factor of order unity, and therefore the gyro radius in Fig. 2 is also approximately the same as c/w pi. The gyro radius re (and thus c/w pe) is smaller than the gyro radius ri by a factor of (mi/me)1/2. The Debeye length l D has the same density dependence as the electron gyro radius. Therefore the variation of all the usual characteristic lengths with density is correctly inferred from Fig. 2, and a reasonable conjecture is that the tendency towards smaller size at higher density is true for anomalous transport as well as for classical transport.
III. Plasma Energy Reduced at High Density
To quantify the variation of diffusion step sizes with density in terms that come closer to economic value, we show in Fig. 3 the thermal energy contained by a plasma with characteristic dimension of a. Three different configurations are included in Fig. 3: ICF-relevant unmagnetized fuel, tokamaks, and a generic MTF plasma taken to be a compact torus (CT). We assume that when density is varied for a given configuration, size is adjusted to be the minimum necessary to provide nt E = 3x1014 cm-3 sec at 10 keV temperature. Specific assumptions for each configuration are summarized in the table following Fig. 3.
A. ICF Energy Requirements
For ICF we see a very strong dependence of energy upon density, and thus the importance of compressing to high density. By compressing to density of approximately 1025 cm-3, the energy in the hot spot according to Fig. 3 is approximately 30 kJ, which is similar to the value anticipated in the design of NIF [Lindl 95]. Achieving such a high density requires an implosion velocity of about 30-40 cm per microsecond and a radial convergence of between 30 and 40. The NIF laser design, with 1.8 MJ and 500 TW, has enough energy and power to produce these conditions even with the inefficiency of indirect drive. However, if the hot-spot density were to be reduced, the energy requirements would be considerably increased as shown in Fig. 3, and the power requirements would also be increased to achieve the same nt E. Thus, the ICF approach utilizes very high density to achieve fusion with minimum energy, but the driver requirements are extremely demanding and expensive.
B. Tokamak Energy Requirements
Tokamaks are included in Fig. 3 for academic interest, even though high-density operation of a tokamak-like configuration is not being considered. The poloidal magnetic field required at any given density is plotted in Fig. 2. For the assumed value of safety factor (q) and aspect ratio, the toroidal field required would be approximately a factor of ten higher than the poloidal field. Thus, the magnetic energy would be 100 times as large as the plasma thermal energy plotted in Fig. 2. The cost of a tokamak is well known to be strongly tied to the cost of the magnets.
The important aspect of the tokamak is that much more is known about transport than for any other configuration. A useful summary of tokamak transport formulas can be found in the textbook by Kadomtsev [Kadomtsev 92]. We plot both the classical limit for confinement (neoclassical in the banana, transition, and Pfirsch-Schluter regimes as density increases) and some empirically based models for anomalous transport. The anomalous transport curves show the anticipated tendency that system size becomes small at increasing density. One concludes from these plots that if the technology were available to operate tokamaks at higher density, the size and cost could be reduced.
C. MTF Energy Requirements.
For MTF compression by a liner, there are many possible magnetic configurations. To make estimates for Fig. 3, we have chosen a compact toroid (CT) plasma as generic for any magnetic configuration. Specifically the CT curves in Fig. 3 are calculated assuming the plasma is an FRC, which has ideally only poloidal magnetic field [Tuszewski 88]. Similar values apply to a spheromak. In that case a toroidal field comparable in magnitude to the poloidal field of the FRC would be required [Jarboe 94]. CTs require more energy than a tokamak at a given density because CTs need more volume to achieve the same effective radius or insulating distance. A prolate FRC, as is commonly studied in experiments, has an effective radius equal to the distance from the field null to the outer edge, which is approximately 0.3 of the small radius of the prolate spheroid. Thus the FRC estimate for energy may be conservatively high in Fig. 3, although modeling of wall-plasma interactions tend to show spatial profiles that resemble an FRC-like profile (Siemon 97).
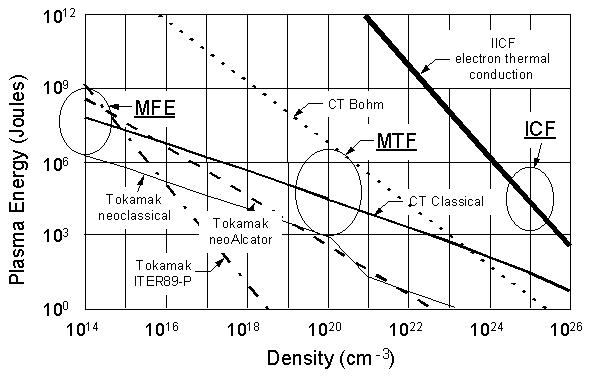
Figure 3. Energy requirements vs. fuel density for various configurations and transport assumptions assuming nt E = 3x1014 cm-3 sec, T = 10 keV, and poloidal b = 1.
|
Configuration |
Transport |
Comments |
|
ICF |
Electron thermal conduction |
Spherical plasma with size given by Eqn. 12. Density of ~1025 cm-3 corresponds to NIF. |
|
Tokamak |
Neoclassical, anomalous neo-Alcator, and anomalous ITER-89P |
Aspect ratio (2.9), poloidal beta (1.0), and safety factor q (3.0) are held constant at ITER-like values. |
|
Compact Torus (CT) |
Classical or Bohm |
Geometry of a prolate FRC assumed for illustration with length to diameter ratio of 3. |
The amount of energy required for fusion conditions depends upon the global energy confinement time. Fig. 3 indicates that compressed plasma energy between about 30 kJ and 10 MJ is required in the MTF regime (density of 1020 cm-3), if plasma transport is between classical and Bohm. For the larger Bohm requirement of 10 MJ, the required liner kinetic energy would be tens of MJs, a few times the final plasma energy. One striking difference between the MFE and MTF regimes of density is that Bohm is an acceptable possibility at MTF density, while as shown in Fig. 3, Bohm is totally unacceptable at 1014 cm-3.
D. Comments on Bohm Diffusion
The curve labeled Bohm deserves additional comment. In the early days of fusion research Bohm was introduced as an empirical diffusivity [Spitzer 62] equivalent to the following:
c BOHM = c i (w cit ii)/16, (18)
where w cit ii = l /ri is the magnetization parameter. The factor of 16 has no theoretical basis. It is interesting to note that apart from the factor of 16, c BOHM is the geometric mean or logarithmic average of c i and c e given in Eqns. 14 and 15. Thus Bohm can be thought of as intermediate between classical magnetized and unmagnetized confinement. Kadomtsev describes how there are situations where macroscopic convection can lead to energy transport with a global Bohm confinement time [Kadomtsev 92]. Studies of wall-confined MTF-type plasma by Vekshtein show how classical confinement can lead to a Bohm-like scaling [Vekshtein 90]. Even more interesting is that experimental data from a number of carefully studied magnetic configurations, including Reversed Field Pinches, spheromaks, and FRCs, is generally as good as Bohm or better.
Global energy confinement time can be worse than Bohm when other non-diffusive processes dominate. Examples are radiation because of impurities, or plasma flow out of the system at a speed comparable to the thermal speed. Radiation by impurities is always a concern and places an upper limit on the allowed impurity concentration. Plasma flow cannot be ruled out in general, but the conjecture here is that target plasma configurations can be found for which a pressure equilibrium exists between the metal liner boundary and the fuel, and thus flow is reduced to nothing worse than convective motions. Close proximity of a conducting boundary should provide a stabilizing influence on magneto-hydrodynamic modes, especially since magnetic fields do not penetrate a conducting boundary on the short time scale of interest for MTF. Spheromaks and FRCs are two examples of CTs for which there are data to support this conjecture. We conclude Bohm represents a reasonable, even conservative, expectation for achievable global energy confinement based on previous experimental results, assuming impurities can be avoided by careful experimental technique.
IV. The Size and Cost of Ignition Facilities
Only a rough connection can be made between cost and plasma energy plotted in Fig. 3. For each of the configurations, however, one would expect that the indicated reduction of energy as density increases would result in a reduction of costs for the required facility to create the ignition-grade plasma. Even an approximate connection is adequate for present purposes, given the many decades of system size plotted in Fig. 3. Note that the left-hand scale varies by 12 orders of magnitude. We list in Table 1 costs for recently designed ignition-class facilities in each of the regimes of MFE, ICF, and MTF.
In the case of MTF we base the cost for an ignition facility upon the ATLAS pulsed-power facility, recently designed and under construction by Defense Programs at Los Alamos [Trainor 97]. ATLAS should be able to deliver 5-10 MJ to an imploding liner, which makes it suitable for a considerable range of possible MTF experiments. Although the primary mission of ATLAS is not MTF, a reasonable number of additional experiments to test MTF are consistent with current plans for the facility. For the purpose of estimating MTF ignition-grade facility costs, we assume that 1) the 35-MJ of stored energy in ATLAS is enough to implode a liner-plasma configuration to ignition (see Fig. 3), and 2) the additional cost for the plasma target preparation is small compared with the $50-million cost of the ATLAS facility. The purpose of Table I is to compare facility costs needed for a fusion energy development program. The fact that ATLAS is being built for other reasons is simply a fortunate circumstance. The research effort expended to date on MTF has been minuscule compared with the other two approaches to fusion, and so the cost of achieving ignition conditions is obviously much less certain. However, the advantage appears so large that the accuracy of the estimate is not very important.
Table 1. Approximate Cost of Ignition Facilities
|
Concept |
Plasma Thermal Energy |
Facility Cost |
|
MFE/ITER |
1 GJ |
$10 billion |
|
ICF/NIF |
30 kJ |
$1 billion |
|
MTF/ATLAS |
~ 10 MJ |
~$50 million |
V. Near Term Prospects for MTF Research
A. Typical MTF Parameters
The main points of this paper, which are contained in Fig. 3 and Table 1, argue for starting a new thrust in fusion energy research. In this section we discuss some aspects of how to begin that effort. Our concept for a liner-driven plasma implosion suggests approximate values for initial and final plasma parameters as given in Table 2.
Table 2. Representative Conditions for an Adiabatic Implosion
|
Parameter |
Desired Final Conditions |
Required Initial Plasma if Kv=100 |
Required Initial Plasma if Kv=1000 |
|
|
|
|
|
|
Temperature |
10 keV |
460 eV |
100 eV |
|
Density |
1020 cm-3 |
1018 cm-3 |
1017 cm-3 |
|
B Field |
10 MG |
100 kG |
100 kG |
|
Liner inner radius |
5 mm |
5 cm |
5 cm |
To illustrate the required initial target-plasma conditions, we assume adiabatic compression (pVg =const) with a volumetric compression Kv = 100 or 1000, corresponding to cylindrical, or spherical, radial compression of 10 respectively. The adiabatic approximation is justified according to time-dependent calculations taking thermal and radiation losses into account [Lindemuth 83], and the parameter space for MTF is found to be quite large, assuming an implosion velocity on the order of 106 cm/sec.
B. Target Plasma Possibilities.
Among the many possible magnetic configurations that would be possible for the target plasma, the ones currently receiving attention in our awareness are: 1) the MAGO-type of accelerated diffuse-z-pinch plasma [Lindemuth, 96], 2) an expanded high-density-fiber z pinch inside a conducting boundary [Wysocki 97], and 3) compact toroids [Ryutov 96]. An approach that uses energy from a high-power e-beam driver to form a magnetized plasma has also been reported [Chang 78].
Extensive research on compact toroids, the spheromak and Field-Reversed Configuration, began in about 1980. The review articles by Tuszewski and Jarboe have hundreds of references [Tuszewski 88, and Jarboe 94]. By definition, a CT is a self-contained magnetized plasma that can be moved from one spatial location to another. Thus, CTs are an obvious candidate for inserting a plasma target into an imploding metal liner. Unfortunately, most fusion-related liner research ended about the same time that CT work began, so most of the information gained from CT research was not available to the early liner researchers. A few experiments studying the implosion of an FRC-type of CT were done in Russia [Kurtmullaev 82]. Most CT research was done at much lower density than is needed for MTF. The RACE experiments at LLNL are a notable exception [Hammer 91]. There is no obvious problem in forming CTs at higher density, and experiments to move in that direction would be desirable.
The MAGO and expanded fiber z pinch are diffuse z-pinch magnetic configurations. The outstanding attraction of these approaches is that the technology for plasma formation is reasonably compatible with liner implosion technology, and is less complicated than for CTs. For MAGO at least, plasma density and temperature appear suitable for proceeding with MTF implosion experiments [Lindemuth 95]. More refined measurements are still needed to characterize global energy confinement in both the MAGO and expanded fiber plasmas. The diffuse z pinch has well known limitations with regard to stability, and containment of energetic particle orbits. However, simulations show [Sheehey 89] that an unstable plasma inside a conducting boundary can evolve to a stable state (known as a Kadomtsev-stable profile). In such a state, the energy confinement may be adequate on the time scale of an MTF implosion. The fact that most alpha particles generated near peak compression would be lost is not a major consideration for the batch-burn approach we have assumed for MTF.
The advances in liner technology of the past few years are impressive [Chernyshev 97]. More than enough liner velocity and implosion symmetry has been demonstrated compared with the detailed requirements for an MTF liner system discussed elsewhere [Lindemuth 96, Siemon 97, Ryutov 96, and Schoenberg 98]. A quasi-spherical implosion of unmagnetized plasma has also been reported [Degnan 96].
A number of existing facilities supported by DOE’s Defense Programs and DOD would be suitable for a variety of MTF experiments. These include the Z capacitor bank at Sandia National Laboratory, the Shiva Star capacitor bank at Phillips Air Force Laboratory, the Pegasus capacitor bank at Los Alamos National Laboratory, the Ranchero explosively-driven electrical generators at Los Alamos, and the ATLAS capacitor bank under construction at Los Alamos.
These facilities and expertise allow significant leveraging of research dollars, which gives additional incentive for MTF research.
D. Major Technical Issues.
MTF can be conceptually separated into three inter-related aspects: target plasma formation and confinement properties, liner-driver implosion, and target-plasma compression. The major technical issues are:
Issues of Target Plasma Formation and Confinement Properties
Liner-Driver Implosion Issues
Target Plasma Compression Issues
We recommend a multi-institutional MTF research program to address these important experimental and theoretical questions. In addition, studies are needed on how MTF would best be utilized for electricity generation or other applications. Qualitatively the intrinsically pulsed nature of MTF makes it similar to ICF in its potential application. Early studies of an electrical power plant based on liner technology [Krakowski 78] indicated the basic feasibility of a pulsed liner-driven system, and identified numerous technology issues that must be solved.
An intriguing more recent study of power generation using MHD conversion of fusion energy [Logan 93] indicates that MTF is well matched to the requirements of an MHD conversion system. The energy from 14-MeV neutrons would be used to vaporize and heat a lithium-containing blanket to 1 or 2 eV. Then MHD conversion gives higher efficiency and a greatly reduced balance of plant cost leading to considerably less expensive electricity compared with conventional MFE reactor concepts.
VI. Conclusions
We briefly reviewed some very elementary features of all the standard fusion approaches. The main assumptions were that the fusion fuel is deuterium and tritium with a 10 keV Maxwellian velocity distribution. We emphasized the variation of quantities with fuel density and observed that the system size becomes small, and energy requirements are much reduced, when fuel density is made considerably larger than in conventional MFE systems. This general conclusion, which has been noted by many researchers in the past, warrants renewed attention today as the fusion program restructures itself within today’s budget limitations.
The reasons for embarking on an MTF research effort at the present time are several:
The interesting regime we call Magnetized Target Fusion occurs at fuel density of about 1020 cm-3. The MTF regime may be an optimum in the sense of using the maximum possible magnetic field for insulation of the fuel, and thus the smallest possible system size without going to the extreme density of ICF. This new thrust in fusion research has the potential to achieve the lowest possible development cost.
We believe that the arguments presented here are robust in nature and give a valid basis for recommending a new research thrust in magnetic fusion energy. Given the global importance of long-term energy R&D, adding MTF as a new complementary element to MFE and ICF in the portfolio of fusion approaches seems well justified.
Acknowledgements
We appreciate receiving encouragement to examine MTF from John Browne, Steve Younger, and Al Sattelberger. We also thank our colleagues Carl Ekdahl, Bob Reinovsky, and others in the pulsed power community at Los Alamos for providing expert advice on liner technology.
References
Bangerter 97. R. Bangerter, " The U. S. Heavy Ion Fusion Program," 12th International Symposium on Heavy Ion Inertial Fusion and Workshop on Atomic Physics, Heidelberg, Germany,September 22-27, 1997.
Boozer 83. A. H. Boozer, Phys. Fluids 26, 496 (1983).
Chang 78. J. Chang, M. M. Widner, A. V. Farnsworth, R. J. Leeper, T. S. Prevender, L. Baker, J. N. Olsen, in High Power Electron and Ion Beam Research and Technology (Proc. 2nd Int. Top. Conf. Ithaca, NY, 1977) Vol.1, Cornell University (1978) 195.
Chernyshev 97. V. K. Chernyshev, "Study of Condensed High Energy Liner Compression," 11th International Pulsed Power Conference, Baltimore, Maryland, June 1997, and other papers of this conference.
Degnan 96. J. H. Degnan, S. K. Coffey, D. G. Gale, J. D. Graham, et. al., "Solid spherical and cylindrical shell z-pinches used to compress hot hydrogen working fluid," 1996 IEEE international conference on plasma science, June 3-5, Boston (1996), 43. Also, J. H. Degnan, F. M. Lehr, J. D. Beason, G. P. Baca, D. E. Bell, A. L. Chesley, S. K. Coffey, D. Dietz, D. B. Dunlap, S. E. Englert, T. J. Englert, D. G. Gale, J. D. Graham, J. J. Havranek, C. D. Holmberg, T. W. Hussey, R. A. Lewis, C. A. Outten, R. E. Peterkin, D. W. Price, N. F. Roderick, E. L. Ruden, U. Shumlak, G. A. Smith, P. J. Turchi, Phys. Rev. Ltrs. 74, 98 (1995).
Gerwin 79. R. A. Gerwin, R. C. Malone, "Adiabatic Plasma Heating and Fusion-Energy Production by a Compressible Fast Liner," Nucl. Fusion 19(2), 155 (1979).
Gross 76. B. Feinberg, "An experimental study of hot plasma in contact with a cold wall," Plasma Physics 18, 265 (1976). =
Hammer 91. J. H. Hammer, J. L. Eddleman, C. W. Hartman, H. S. McLean, A. W. Molvig, "Experimental demonstration of compact torus compression and acceleration," Phys Fluids B 3, 2236 (1991).
Holdren 95. The U.S. Program of Fusion Energy Research and Development, The President’s Committee of Advisors on Science and Technology (PCAST), "Report of the Fusion Review Panel," J. Holdren, Chairman, (July 1995).
Jarboe 94. T.R. Jarboe, "Review of spheromak research," Plasma Phys. Control. Fusion 36, 945 (1994).
Kadomtsev 92. B. B. Kadomtsev, Tokamak Plasma: A Complex Physical System, (Institute of Physics Publishing, Bristol and Philadelphia, 1992).
Krakowski 78. R. W. Moses, R. A. Krakowski, R. L. Miller, "A conceptual design of the fast-liner reactor (FLR) for fusion power," Los Alamos Scientific Laboratory informal report, LA-7686-MS (1979) [available on LANL library web site].
Kurtmullaev 1980. S. G. Alikhanov, V. P. Bakhtin, A. G. Es’kov, R. Kh. Kurtmullaev, V. N. Semenov, E. F. Strizhov, N. P. Kozlov, V. I. Khvesyuk, A. V. Yaminskij, "Three-dimensional Plasma Compression in a Z-Pinch Liner System – Transport and Compression of a Compact Torus by a Quasi-Spherical Liner, 8th IAEA Fusion Energy Conference III, 319 (1982).
Lindemuth 83. I. R. Lindemuth, R. C. Kirkpatrick, "Parameter space for magnetized fuel targets in inertial confinement fusion," Nuclear Fusion 23(3), (1983).
Lindemuth 95. I. R. Lindemuth, et.al., "Target Plasma Formation for Magnetic Compression/Magnetized Target Fusion," Phys. Rev. Ltrs. 75(10), 1953-1956 (September 1995).
Lindemuth 96. I. Lindemuth, C. Ekdahl, R. Kirkpatrick, R. Reinovsky, R. Siemon, P. Sheehey, F. Wysocki, V. Chernyshev, V. Mokhov, A. Demin, S. Garanin, V. Korchagin, I. Morozov, V. Yakubov, J. Eddleman, J. Hammer, D. Ryutov, A. Toor, D. McDaniel, J. Degnan, G. Kiuttu, R. Peterkin, Jr., "Magnetic Compression / Magnetized Target Fusion (MAGO/MTF): A Marriage of Inertial and Magnetic Confinement," 16th IAEA Fusion Energy Conference, Montreal, Canada, October 7-11, 1996.
Lindl 95. J. Lindl, "Development of the Indirect-Drive Approach to Inertial Confinement Fusion and the Target Physics Basis for Ignition and Gain," Phys. of Plasmas 2(11), 3933-4024 (November 1995).
Logan 93. B. G. Logan, "Inertial Fusion Reactors using Compact Fusion Advanced Rankine (CFARII) MHD Conversion," Fusion Engineering and Design 22, 151-192 (1993).
Pavlovskii 96. Paper at Megagauss V (1996)
Robson 76. A. E. Robson, P. J. Turchi, "NRL Linus Program," Pulsed high beta plasmas (3rd topical conference on pulsed high beta plasmas, Pergamon Press, Oxford, 1976), 477. Also: P. J. Turchi, Review of the NRL Liner Implosion Programme, Megagauss Physics and Technology (Plenum Press, New York, 1980), 375
Ryutov 96. R. P. Drake, J. H. Hammer, C. W. Hartman, L. J. Perkins, D. D. Ryutov, "Submegajoule Liner Implosion of a Closed Field Line Configuration," Fusion Tech. 30, 310-325 (1996).
Schoenberg 98. K. Schoenberg et. al., "Application of the ATLAS facility to MTF Experiments," to be published.
Sheehey 89. P. Sheehey, "Computational Modeling of Wall-supported Dense Z-Pinches," Proc. of Second International Conference on Dense Z-Pinches, Laguna Beach, California, April 26-28, 1989.
Sheffield 94. J. Sheffield, The physics of magnetic fusion reactors, Reviews of Modern Physics 66(3), 1015 (1994).
Sherwood 81. A. R. Sherwood and F. L. Ribe, "Fast-Liner-Compression Fusion Systems," Fusion 1, Part B, 59-78 (1981).
Siemon 97. R. E. Siemon, "Magnetized Target Fusion - A High-Density Pulsed-Power Approach to Fusion," Los Alamos National Laboratory talk LA-UR-97-764, presented at the Innovative Confinement Concepts Workshop, Marina del Rey, California, March 3-6, 1997.
Spitzer 62. L. Spitzer, Physics of Fully Ionized Gases (Interscience Publishers, New York & London, 1962), p. 47.
Trainor 97. J. Trainor, et. al., "Overview of the Atlas Project," Proc. of 11th IEEE International Pulsed Power Conference (Baltimore, MD, June 29- July 2, 1997, to be published).
Tuszewski 88. M. Tuszewski, "Field Reversed Configuration," Nuclear Fusion 28(11), 2033-2092 (1988).
Vekshtein 90. G. E. Vekshtein, "Magnetothermal Processes in Dense Plasma," Rev. Plas. Physics 15, 1 (1990).
Wysocki 97. F. J. Wysocki, R. E. Chrien, G. Idzorek, H. Oona, D. O. Whiteson, R. C. Kirkpatrick, I. R. Lindemuth, and P. T. Sheehey, "Progress With Developing A Target For Magnetized Target Fusion", Proc. of 11th IEEE International Pulsed Power Conference (Baltimore, MD, June 29- July 2, 1997, to be published).